
Abstract -- Trying to identify a melody from just a few bars? Some tune buzzing round your head, bugging you? If you ever want to discover a song's name but can only remember a few notes, the New Zealand Digital Library's Web-based melody index is the service for you! You can sing (or hum, or play) a few notes and search for the tune in a database of 9,400 folk songs. You get back the notes you sang in musical notation, along with a ranked list of matching tunes. You can listen to the melodies, view them in musical notation, and download them in a variety of popular formats.
This paper describes the MELDEX system, designed to retrieve melodies from a database on the basis of a few notes sung into a microphone. It accepts acoustic input from the user, transcribes it into the ordinary music notation that we learn at school, then searches a database for tunes that contain the sung pattern, or patterns similar to it. Retrieval is ranked according to the closeness of the match. A variety of different mechanisms are provided to control the search, depending on the precision of the input. This article presents an analysis of the system's performance using different search criteria involving melodic contour, musical intervals and rhythm. Tests were carried out using both exact and approximate string matching. Approximate matching uses a dynamic programming algorithm designed for comparing musical sequences.
Music librarians are often asked to find a piece of music based on a few sung or hummed notes. The magnitude of this task may be judged by the fact that the Library of Congress holds over six million pieces of sheet music (not including tens of thousands of operatic scores and other major works), and the National Library of France has 300,000 hours of sound recordings, 90% of it music. As digital libraries develop, these collections will increasingly be placed on-line through the use of optical music recognition technology.
The New Zealand Digital Library's MELody inDEX (MELDEX) system retrieves music on the basis of a few notes that are sung, hummed, or otherwise entered. Users can literally sing a few bars and have all melodies containing that sequence of notes retrieved and displayed -- a facility that is attractive to casual and professional users alike. Such systems will form an important component of the digital music library of the future. With them, researchers will analyze the music of given composers to find recurring themes or duplicated musical phrases, and musicians and casual users alike will retrieve compositions based on remembered (perhaps imperfectly remembered) musical passages.
Capitalizing on advances in digital signal processing, music representation techniques, and computer hardware technology, our system transcribes melodies automatically from microphone input. It then searches a database for tunes containing melodic sequences similar to the sung pattern, and ranks the tunes that are retrieved according to the closeness of the match. We have implemented different search criteria involving melodic contour, musical intervals and rhythm; carried out tests using both exact and approximate string matching; and performed user studies on how people remember tunes. We conclude from these experiments that people need a choice of several matching procedures and should be able to explore the results interactively in their search for a particular melody; this is exactly what the MELDEX system offers.
It is necessary to have a database of tunes stored in the form of music notation, and our test database is a collection of 9,400 international folk tunes. One current limiting factor is that few score collections are available in machine-readable form. As digital libraries develop, however, scores will be placed online through the use of optical music recognition technology, and we are planning to expand our database in this way. Furthermore, with the increasing use of music notation software, many compositions will be acquired in electronic form -- particularly by national libraries, which acquire material through copyright administration.
The front end of our music retrieval system performs the signal processing necessary to automatically transcribe a melody from audio input. The user specifies a URL (or a file) that contains a sampled acoustic signal. This is transferred to our site. There the sung notes are segmented from the acoustic stream; their frequency is identified and pitch labels are assigned; and the duration of each note is calculated.
For music transcription, we are interested only in the fundamental frequency of the input. Therefore the input is filtered to remove as many harmonics as possible, while preserving the fundamental frequency. First we convert the input file to a standard sample rate of 22 kHz, quantised to an 8-bit linear representation. Reasonable limits for the singing voice are defined by the musical staff, which ranges from F2 (87.31 Hz) just below the bass staff, to G5 (784 Hz) just above the treble staff. Input is low-pass filtered, with a cutoff frequency of 1000 Hz, then passed to the pitch tracker, which identifies pitch by finding the repeating pitch periods which make up the waveform (Gold & Rabiner 1969). Figure 1 shows 20 ms of a typical waveform for the vowel ah, as in father. The pitch tracker returns an average pitch estimate for each 20 ms segment of input; this gives the system a pitch resolution of approximately five cents (a cent is one hundredth of a semitone). This is about 0.29%, and approximates human pitch resolution.
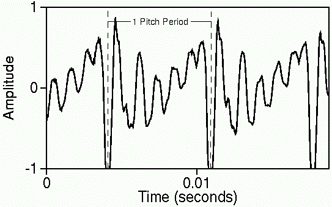
Figure 1. Acoustic waveform of ah
Once pitches have been identified, it is necessary to determine where notes begin and end. Our system depends on the user separating each note by singing da or ta -- the consonant causes a drop in amplitude of 60 ms duration or more at each note boundary. Adaptive thresholds are then used to determine note onsets and offsets; in order to keep a marginal signal from oscillating on and off, the onset threshold is higher than the offset threshold. Figure 2 illustrates the use of amplitude to segment a series of notes. We have investigated the segmentation of notes based solely on the pitch track, but this method is not yet as reliable as segmentation based on amplitude.
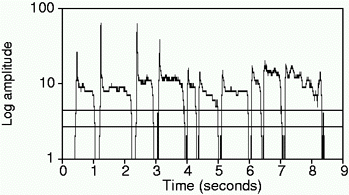
Figure 2. Amplitude segmentation
Whether or not note durations are taken into account during matching is a matching option for advanced queries. After note onsets and offsets are determined, rhythmic values are assigned by quantising each note to the nearest minimum note duration set by the user. In order to permit this, the user must supply the metronome speed, and the minimum note and rest durations, as a transcription option when issuing an advanced query. For simple queries, these options are set to reasonable defaults.
Transcription of Western music requires that each note be identified to the nearest semitone. For several reasons, however, it is desirable to represent pitches internally with finer resolution. Our system expresses each note, internally, by its distance in cents above 8.176 Hz, or MIDI note 0. Notes on the equal tempered scale, relative to A-440, occur at multiples of 100 cents; C4, or middle C, is 6000 cents, while A4, or concert A, is 4400 cents. This scheme easily incorporates alternative (non-equitempered) tunings of Western music, such as the "just" or Pythagorean system, simply by changing the relationship between cents and note name. It can also be easily adapted to identify notes in the music of other cultures.
Our system labels each note according to its frequency and a reference frequency. In some applications, it is desirable to tie note identification to a particular standard of tuning, such as A-440. For a melody retrieval application, however, it is often desirable to adapt to the user's own tuning and tie note identification to musical intervals rather than to any standard. This is provided as a transcription option for advanced queries.
With adaptive tuning, the system begins a transcription with the assumption that the user will sing to A-440, but then adjusts by referencing each note to its predecessor. For example, if a user sings three notes, 5990 cents, 5770 cents and 5540 cents above MIDI note 0, the first is labeled C4 and the reference is moved down 10 cents. The second note is labeled Bb3, which is now referenced to 5790 (rather than 5800) cents, and the reference is lowered a further 20 cents. The third note is labeled Ab3, referenced now to 5570 cents--even though, by the A-440 standard, it is closer to G3. Thus the beginning of Three Blind Mice is transcribed.
Retrieving music from a collection of musical scores is essentially a matter of matching input strings against a database. This is a familiar problem in information retrieval, and efficient algorithms for finding substrings in a body of text are well known. Unfortunately, there are several problems with seeking an exact match between the transcribed melody and the database. The first is the variability in the way that music is performed. Folk songs, for example, appear in many variants, while popular songs and well-known standards are often performed differently from the way they are notated. Performances of classical music generally have a more stable relationship to the score, but there are other sources of error. Problems may be caused by deficiencies in the user's singing -- or his or her memory of the tune may be imperfect. We have performed an experiment to determine the accuracy of people in singing well known songs (McNab et al. 1996), and our findings indicate that people make a number of mistakes in singing intervals and rhythms of songs, even when those songs are well known to them.
It is necessary, then, to allow approximate string matching on the score database in order to retrieve music. Approximate matching algorithms are, in general, far less efficient than those that match strings exactly, and invariably take time which grows linearly with database size rather than logarithmically, as does binary search.
It is necessary to decide whether to constrain the matching to start at the beginning of songs, or whether to permit matching at any point within a song. In our preliminary experiment, most subjects started at the beginning of the song. However, on one of the commercial popular songs, most subjects started at the chorus. The structure of modern popular music, where songs are designed with a memorable "hook" line to capture listeners, means that singers are likely to start at the hook -- which often occurs at the beginning of the chorus -- rather than at the beginning of a song. Rather than attempt to identify the "hook" line for each tune in our database, we made the question of whether to match at the start of tunes only, or anywhere within the tune, a matching option for advanced queries.
What attributes should be used when searching a musical score database? The first point to note is that melodies are recognizable regardless of the key in which they are played or sung -- so it is important to allow users to enter notes in any key. This is accomplished simply by conducting the search on the basis of pitch ratios, or musical intervals. Second, a number of experiments have shown that interval direction, independent of interval size, is an important factor in melody recognition (Dowling 1978) -- indeed, Parsons (1975) has produced an index of melodies based entirely on the sequence of interval directions, which is called the "melodic contour" or "pitch profile." Using the notation of Parsons, where * represents the first note, D a descending interval, U an ascending interval, and R a repetition, the beginning of Three Blind Mice is notated: *DDUDDUDRDUDRD
One cardinal advantage of searching on contour, at least for casual singers, is that it releases them from having to sing accurate intervals. The MELDEX system uses contour matching as a default, with interval matching provided as a matching option for advanced queries.
Approximate string matching is a standard application of dynamic programming. In general, two strings of discrete symbols are given, and the problem is to find an economical sequence of operations that transforms one into the other. The basic operations are deletion of a single symbol, insertion of a single symbol, and substitution of one symbol by another. These three operations have associated numeric "costs," or "weights," which may be fixed or may depend on the symbols involved. The cost of a sequence of operations is the sum of the costs of the individual operations, and the aim is to find the lowest-cost sequence that accomplishes the desired transformation. The cost of this sequence is a measure of the distance between the strings. Using dynamic programming, the optimal solution can be found in a time which is proportional to the product of the lengths of the sequences.
Mongeau and Sankoff (1990) adapt dynamic programming to music comparison by adding two music-related operations: consolidation, which combines a sequence of notes into one whose duration is their sum and whose pitch is their average (computed with respect to the distance metric), and fragmentation, which does the reverse. While Mongeau and Sankoff designed their algorithm to compare complete melodies, it is necessary for a general music retrieval system to allow a search for embedded patterns, or musical themes. This capability is incorporated into the dynamic programming algorithm by modifying the start condition so that deletions preceding the match of the pattern receive a score of 0.
Using dynamic programming for matching against a large database is naturally rather slow. For example, on a PowerPC 8500 with a clock speed of 120 MHz, pitch tracking of audio input takes approximately 2.8% of recorded time; a typical brief input sample is processed in around 200 ms. Exact matching of the same sample on the 9400 song database takes about 500 ms, but approximate matching can take much longer. Matching a 20 note search pattern, for example, requires approximately 21 seconds. While it may be reasonable to expect a user to wait that length of time for a search to complete, much larger databases--a million folk songs, for example, or a thousand symphonies--will take an unacceptably long time to search.
In order to reduce search time, we have implemented a state matching algorithm for approximate searching (Wu and Manber 1992). Essentially, this involves maintaining k copies of the dynamic programming array, where the ith matrix holds values for matches with up to i errors. Here, k is the number of allowable errors, and for values up to the word size of the computer the algorithm can be implemented efficiently with bitwise logical operations and shifts. The complexity of the method is O(kn+m+a) where n is the length of the pattern, m is the length of the string, and a is the alphabet size. This is much less than the complexity of dynamic programming, O( mn), especially for long search patterns. However, because the technique is based on errors rather than a distance measure, it does not discriminate as well as dynamic programming.
This fast matching technique is used by default, while the slower dynamic programming method can be obtained by setting the matching method to "complex" for advanced queries.
The weaker the matching criteria, the larger the musical fragment that is needed in order to identify a particular song uniquely from a given corpus. To get a feeling for the tradeoffs involved, we performed an extensive simulation based on two corpora of folk songs. The first is a collection of 1,700 tunes, most of North American origin, from the Digital Tradition folksong database (Greenhaus 1994). The other is comprised of 7,700 tunes from the Essen database of European and Chinese melodies (Schaffrath 1992). Combining the two sources gave us a database of 9,400 melodies. There are just over half a million notes in the database, with the average length of a melody being 56.8 notes. In the MELDEX system, the database is divided into the following tune collections:
We are interested in the number of notes required to identify a melody uniquely under various matching regimes. The dimensions of matching include whether interval or contour is used as the basic pitch metric, whether or not account is taken of rhythm, and whether matching is exact or approximate.
Based on these dimensions, we have examined exact matching of:
and approximate matching (using dynamic programming) of:
For each matching regime, we imagine a user singing the beginning of a melody, comprising a certain number of notes, and asking for it to be identified in the database. If it is in the database, how many other melodies that begin this way might be expected? We examined this question by randomly selecting 1,000 songs from the database, then matching patterns ranging from 5 to 20 notes against the entire database. This experiment was carried out both for matching the beginnings of songs and for matching sequences of notes embedded within songs. For each sequence of notes, we counted the average number of "collisions" -- that is, other melodies that match. Fragmentation and consolidation are relevant only when rhythm is used in the match; in these experiments, fragmentation and consolidation were allowed for approximate matching but not for exact matches.
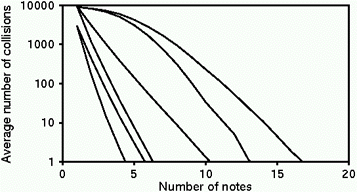
Figure 3. Number of collisions for
different lengths of input
sequence when matching start of song.
|
From left to right: * exact interval and rhythm * exact contour and rhythm * exact interval * exact contour * approximate interval and rhythm * approximate contour and rhythm |
Figure 3 shows the average number of collisions, for each of the matching regimes, when queries are matched at the beginnings of songs. The number of notes required to reduce the collisions to any given level increases monotonically as the matching criteria weaken. All exact-matching regimes require fewer notes for a given level of identification than all approximate-matching regimes. Within each group the number of notes decreases as more information is used: if rhythm is included, and if interval is used instead of contour. For example, for exact matching with rhythm included, if contour is used instead of interval two more notes are needed to reduce the average number of items retrieved to one. The contribution of rhythm is also illustrated at the top of Figure 3, which shows that, if rhythm is included, the first note disqualifies a large number of songs. It is interesting that melodic contour with rhythm is a more powerful discriminator than interval without rhythm; removing rhythmic information increases the number of notes needed for unique identification by about three if interval is used and about six if contour is used. A similar picture emerges for approximate matching except that the note sequences required are considerably longer.
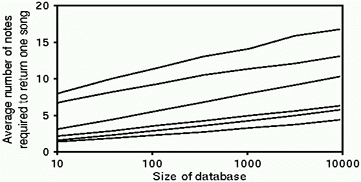
Figure 4. Number of notes for unique
tune retrieval in databases of different sizes.
Lines correspond, from
bottom to top, to the matching regimes listed in Figure 3.
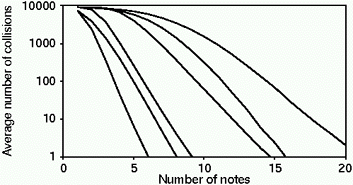
Figure 5. Number of collisions for different lengths of input sequence when matching embedded patterns. Lines correspond, from left to right, to those in Figure 3.
An important consideration is how the sequence lengths required for retrieval scale with the size of the database. Figure 4 shows the results, averaged over 1,000 runs, obtained by testing smaller databases extracted at random from the collection. The number of notes required for retrieval seems to scale logarithmically with database size.
Figure 5 shows the average number of collisions for matching embedded note patterns. As expected, all matching methods require more notes than searches conducted on the beginnings of songs. In general, an additional three to five notes are needed to avoid collisions, with approximate matching on contour now requiring, on average, over 20 notes to uniquely identify a given song.
Figure 6 shows two screen displays from our melody retrieval system. In each case the input file was Auld Lang Syne from the MELDEX demonstration page. For the query on the left, the simple query mode was used. The transcribed input is shown at the top, and titles of tunes returned by the database search appear below. Tunes are ranked according to how closely they match the sung pattern. Any of the returned tunes may be selected for display, and the user can listen to the displayed tune.
 |
 |
In all cases, tunes with a score of 90% or higher are returned. (Although it would be easy enough to provide control over this cutoff level, we have not yet found any real reason to do so.) The precision of the match can be more usefully controlled using the advanced query mode, whose elements have each been described in the sections above. The search on the left of Figure 6 returned tunes 609 songs. However, using interval instead of contour matching on the same input sample yields the page shown at the right of Figure 6, where only nine tunes are returned. In practice, with a query like this it is likely that the user would restrict the search to the North American folksong collection, in which case 74 songs would be returned by the simple query on the left and just one by the more focused query on the right.
Table 1 shows the number of songs returned using the search pattern of Figure 6 for a selection of matching methods. The effect of exact matching can be achieved in the present interface by issuing the corresponding approximate-matching query and counting the number of hits returned at the 100% level. Most of the approximate matching schemes return a manageable number of tunes. However, when embedded matches are sought, approximate matching of contour for this search pattern returns over half the database.
| Search Criteria | Number of Songs Returned | ||
|---|---|---|---|
|
Matching from beginning |
Matching embedded pattern |
||
| Exact matching | Interval and rhythm | 1 | 1 |
| Contour and rhythm | 1 | 3 | |
| Interval | 7 | 8 | |
| Contour | 24 | 515 | |
| Approximate matching | Interval and rhythm | 1 | 2 |
| Contour and rhythm | 2 | 12 | |
| Interval | 9 | 23 | |
| Contour | 609 | 5284 | |
Table 1. Number of songs retrieved using the query of Figure 6
MELDEX is a novel scheme for audio information retrieval by searching large databases of musical scores. Searching such corpora requires efficient string matching algorithms. Previous experiments on melody recognition suggest that searching should be carried out on the basis of melodic contour and/or musical intervals, and our own experiments suggest that there should be provision for approximate matching of the input, and that the audio transcription module should adapt to the user's musical tuning, which may vary during input.
The time taken to perform approximate matches in large databases of musical scores is a matter for some concern. We have described one way of speeding up these searches: to use a fast approximate search method (Wu and Manber 1992). Another possibility, which we also plan to investigate, is to automatically create, offline, databases of themes which allow fast indexing into the main database. It may be possible, for example, to use the Mongeau and Sankoff algorithm to find recurring themes in symphonies or popular songs; these themes can then be stored in a separate, and much smaller, database.
One practical problem is the difficulty of obtaining databases of tunes in the form of musically notated scores. We are addressing this problem through the use of optical music recognition (Bainbridge and Bell, 1996; Bainbridge, 1997). Soon we hope to offer an optical music recognition service under the auspices of the New Zealand Digital Library, whereby music submitted for processing will automatically be added into the database of tunes that can be searched using MELDEX.
Our investigations have focused on retrieval of musical scores. While it may someday be feasible to directly match acoustic input against digital audio files, it is likely that the musical score will be an intermediary representation for some time to come. We envision a system where the user might whistle the theme to Grieg's Piano Concerto in A Minor; this input is then matched to a database of musical themes, and the corresponding recording is returned to the user's terminal. We believe that acoustic interfaces to online music databases will form an integral part of the digital music library of the future.
Bainbridge, D. (1997) Extensible optical music recognition. PhD thesis, Department of Computer Science, University of Canterbury, New Zealand.
Dowling, W. J. (1978) Scale and contour: two components of a theory of memory for melodies. Psychological Review 85: 341354.
Gold, B., and Rabiner, L. (1969) Parallel processing techniques for estimating pitch periods of speech in the time domain. J. Acoustical Society of America 46: 442-448.
Greenhaus, D. (1994) About the Digital Tradition. http://www.deltablues.com/DigiTrad- blurb.html.
Schaffrath, H. (1992) The ESAC databases and MAPPET software. In Computing in Musicology, Vol 8., edited by W. Hewlett and E. Selfridge-Field. Menlo Park, Calif.: Center for Computer Assisted Research in the Humanities.
McNab, R.J., Smith, L.A., Witten, I.H., Henderson, C.L., and Cunningham, S.J. (1996) Towards the digital music library: tune retrieval from acoustic input. In Proceedings of ACM Digital Libraries '96, 1118.
Mongeau, M., and Sankoff, D. (1990) Comparison of musical sequences. Computers and the Humanities 24: 161175
Parsons, D. (1975) The directory of tunes and musical themes. Cambridge: Spencer Brown.
Wu, S., and Manber, U. (1992) Fast text searching allowing errors. Communications of the ACM 35(10), 8391.
One typographical error has been corrected at the request of the authors. Ed., May 16, 1997


hdl:cnri.dlib/may97-witten